Accuracy of Rsqrt and Weird Shadows in Ray Tracing

Almost one and a half years ago, when I was learning Rust, I wrote a ray tracer based on the widely-known textbook “Ray tracing in one weekend”. The book is great and it only took me two days to write the ray tracer. And I found something a bit weird when I tried to optimize it. I’ve looked into the causes of that a while ago, but this time I’m going to take it a little further.

Background: rsqrt instruction

In the 3D CG field, there is a popular optimization technique called fast inverse square root. It is a fast approximation of \(1/\sqrt{x}\) that is computed when we regularize the length of a vector.

Nowadays, most x86_64 CPUs implement rsqrtss instruction that have higher accuracies. By replacing sqrt and division with rsqrtss, we would gain some speedup.

In Rust, you can call intrinsic functions via std::arch::x86_64. To find out what the instructions do, Intel Intrinsics Gude is helpful.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

use std::arch::x86_64::_mm_set_ss;
use std::arch::x86_64::_mm_rsqrt_ss;
use std::arch::x86_64::_mm_cvtss_f32;

impl Vector3 {
    pub fn rlen(self) -> f32 {
//         original implementation
//         1.0 / self.len()
        let lsq = self.len_sq();
        unsafe {
            _mm_cvtss_f32(_mm_rsqrt_ss(_mm_set_ss(lsq)))
        }
    }
}

When I made this change and ran it again, the image looked like the following.

You can see that there are ring-shaped shadows that were not seen in the image shown before. From the concentric pattern, we can assume that the artifacts are due to the length of the ray emitted from the camera. Since the code regularizes all the rays, I guessed the numerical error in rsqrtss causes this. Actually, the artifacts disappear when I replaced rsqrtss by normal division and square root.

Observation: pattern of errors

If a ray tracer overestimates the length of the ray, the position where the ray hits the object becomes distant and would be buried inside the object. A ray that starts from the inside of an object never escapes from it unless it is transparent (A). This is not distinguishable from the case when the ray does not hit to a light source (B), so the pixel would look like a shadow. It may make the pixel darker.

To test this hypothesis, “numerical errors in rsqrtss when calculating the length of rays cause the artifacts”, I plotted the numerical error in a similar way as the ray tracing. I calculated the length of the rays from the camera to the screen and plotted the relative error in the log scale only when the rsqrtss overestimates the length.

The pattern is more intricate than I expected.

Come to think of it, I used some tricks to reduce the noise in ray tracing. For example, I averaged the color from several rays that pass through different points in the pixel. By this operation, the local patterns of the numerical error may disappear.

To check this, I modified the code so that the rays always pass through the center of the pixel. Then the pattern of the artifacts appears almost match the pattern of numerical errors.

Also, there is always an error in floating-point operation, so the collisions that occur immediately after a ray is emitted are normally ignored. In the image shown above, I used \(10^{-5}\) as tolerance. If the overestimate causes the artifacts, larger tolerance makes the artifacts fainter, and vice versa.

Let’s set the tolerance to 0.

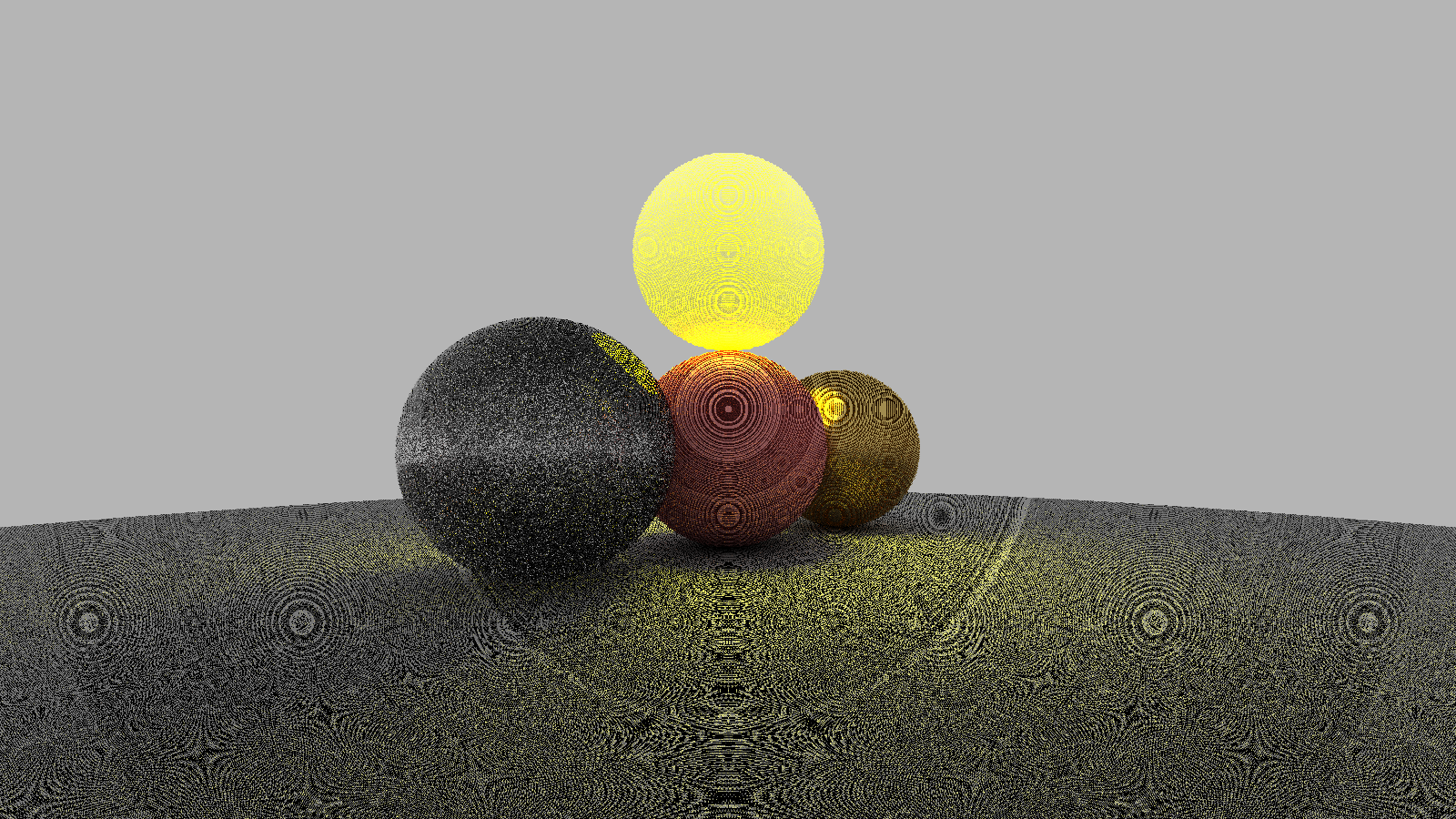
Conversely, let’s make it larger, like 0.05, so that the artifacts almost disappear.

It looks okay at first glance. But you can see that some part of the real shadows becomes a bit brighter. For example, the shadow under the pink sphere located at the center looks pink.

Conclusion

From these observations, it seems that trying to address the problem by increasing tolerance will lead to other problems. So the most obvious solution would be to stop using rsqrt. But there is another way.

The original algorithm of the fast inverse square root is a combination of bit operations and floating-point operations. The floating-point operations correspond to Newton’s method. Starting from the approximation derived by bit operations, it increases the accuracy of the result. The same method can be applied to this case.

1
2
3
4
5
6
7
8
9

impl Vector3 {
    pub fn rlen(self) -> f32 {
        let lsq = self.len_sq();
        let r = unsafe {
            _mm_cvtss_f32(_mm_rsqrt_ss(_mm_set_ss(lsq)))
        };
        r * (1.5 - lsq * 0.5 * r * r)
    }
}

… and the artifacts disappeared!

Unfortunately, I couldn’t find any significant difference in the run time performance between the normal sqrt() version and this in one execution. So the best solution, considering both performance and readability, might be to use 1 / sqrt(x), not rsqrt. But the result may change in another situation, like with SIMD instructions or on GPU.

I hope this result will help those who are in trouble with weird shadows in ray tracing.