Writing board game AI

2020-09-04 about 6319 words 13 min

Contents

SEPAROというゲームをご存知でしょうか。多分、ご存じないでしょう。 SEPAROは、中高時代クラスメイトだったTakeshi Suwaが考案したボードゲームです。私を含む友人たちは当時、教室の黒板でこのゲームを楽しんでいました。

SEPAROは明らかに良く出来たゲームだと思います。 3週間ほど前に突然このゲームのことを思い出して、とても遊びたくなってしまったほどです。とはいえゲームのルールを知っている人がほとんどいないので、私の周囲には遊べる人がいませんでした。

オンラインサーバーを建てることは解決策になり得るでしょうが、それでも、いつでも他のプレイヤーと同時に遊ぶ時間を取れるわけではないという問題は残ります。プレイヤーが少ないほど、マッチングにまつわる問題を解決するのは難しくなります。最もシンプルな解決策は、相手になってくれるプレイヤーを作り出すことでしょう。他の難問と同様、人工知能（AI）がこの問題を解決してくれます。AIは常に暇だからです。

というわけで3週間前にこのボードゲームをプレイするAIを書きました。ここしばらくは忙しく、まとめる時間が取れなかったのですが、ようやくまとまった時間が取れたので思い出しながら書いていくことにします。

背景: SEPAROのルール

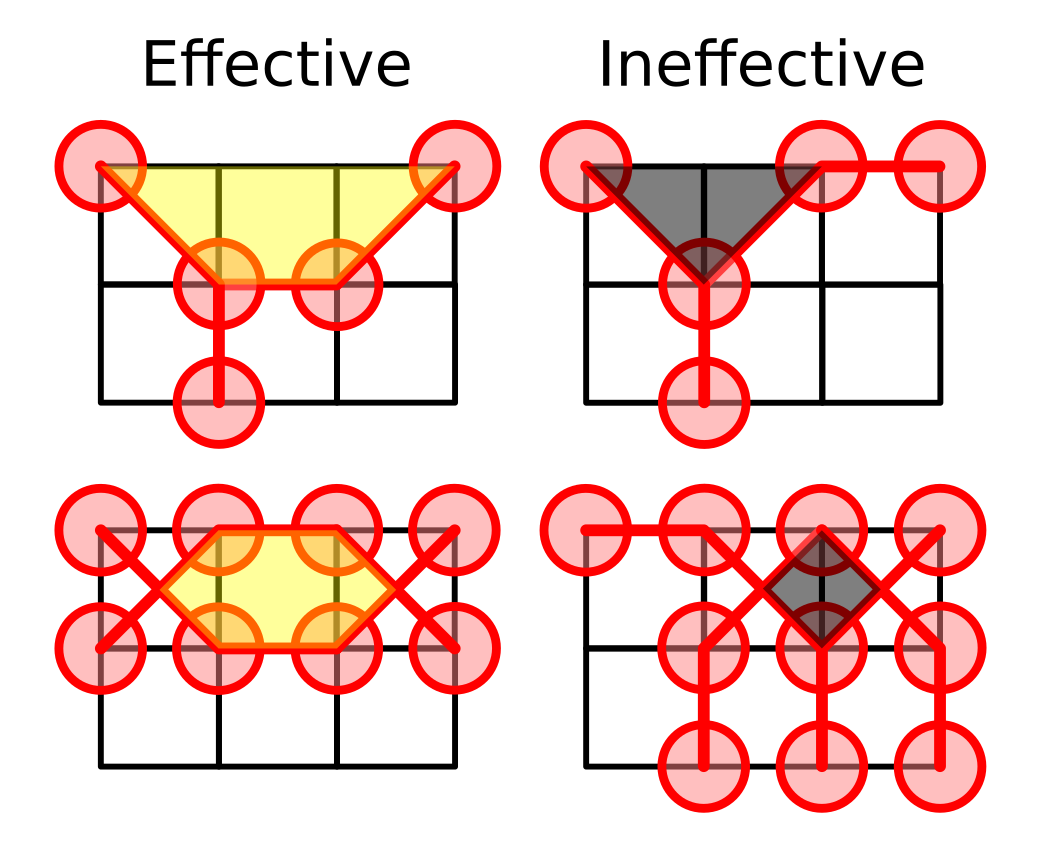
SEPAROは九路盤を使った二人対戦ボードゲームです。 SEPAROでは、プレイヤーは盤面を分割することを目標に戦います。得点は盤面をいくつに分割したかで決まるので、広い陣地を取ることに意味はありません。とはいえ、面積が単位マス以下になるような小さすぎる領域は独立した陣地としてカウントされないことに注意してください。

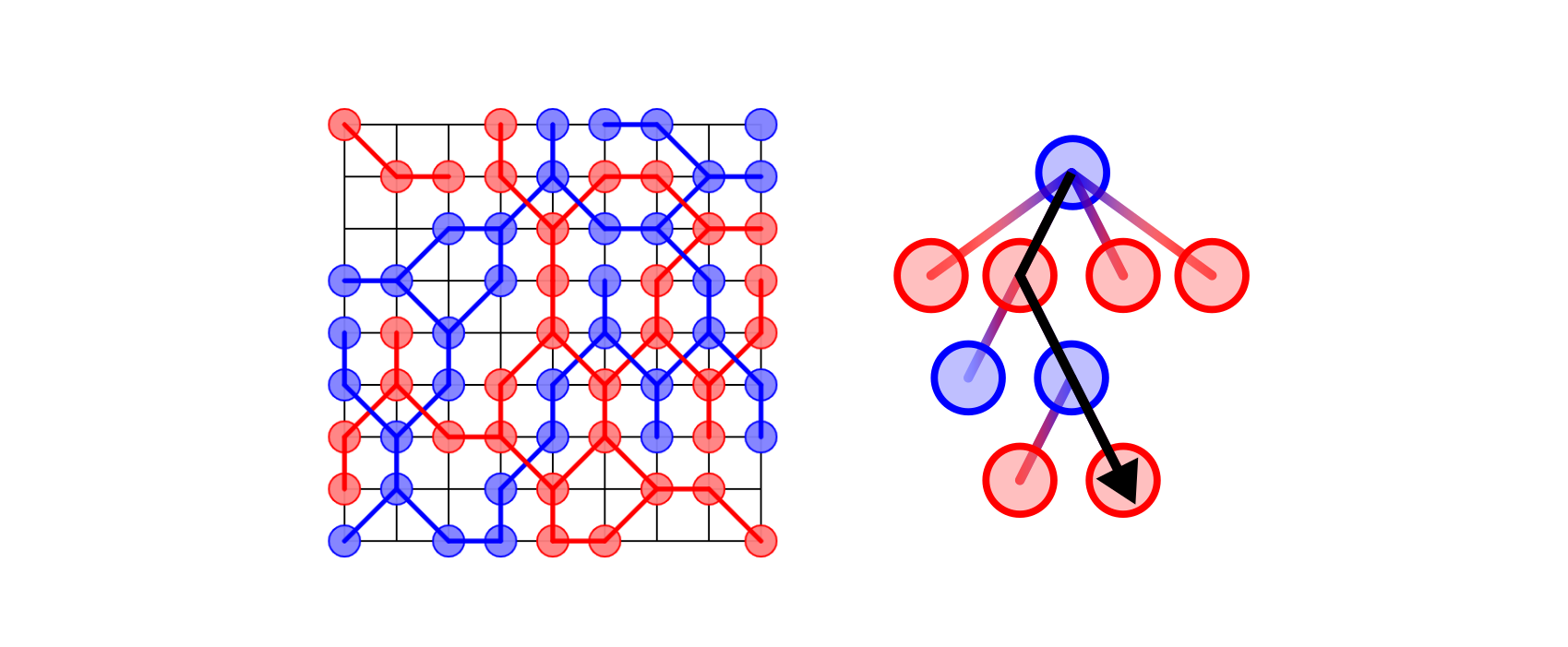
プレイヤーは赤か青の石を使います。赤が先手です。ゲームは双方が次の手を打てなくなるまで続きます。

プレイヤーは交互に石を繋ぐ2本の「根」を伸ばしていきます。石は交点に置き、根は既存の石から以下の法則で伸ばします。

一本目の根は斜めにしか伸ばせず、終端には石を置かなければなりません。石を置くときには、そのグリッドが空である必要があります。また、二本目の根は一本目の終端から、グリッドと平行に伸ばさなければなりません。二本目の根の終端には必ずしも石を置く必要はなく、既存の自分の石と接続することができます。最後に重要なルールとして、根同士は45度の角度で交わることができません。

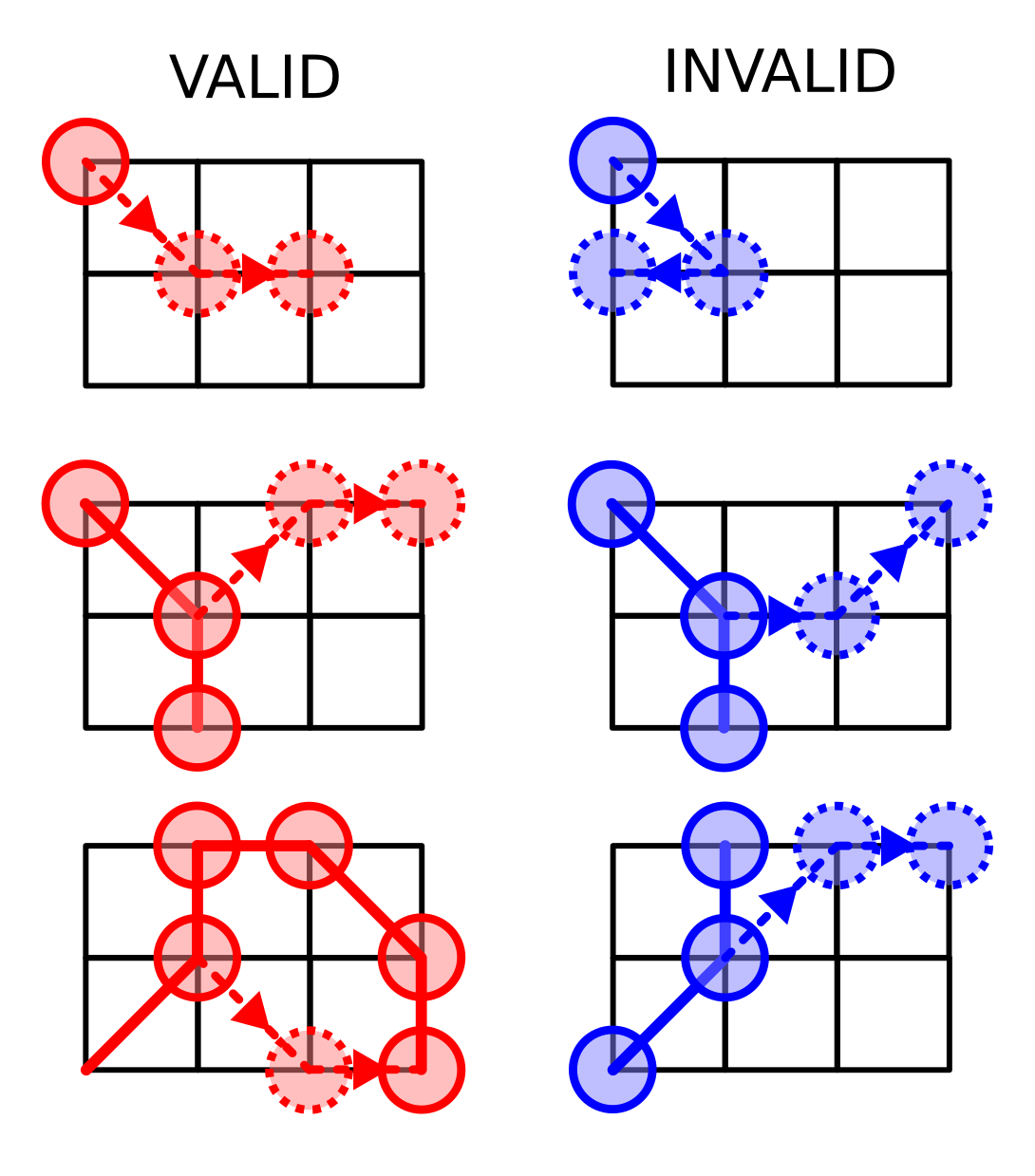
複雑すぎるとお思いでしょうか。でも心配しないでください。今回の実装では伸ばせる手のガイドが表示されるので、自分で探す必要はありません。もしわかりにくければ、AI同士を対戦させて、例を見ることもできます。

以下のウェブサイトで遊ぶことが出来ます。

https://toruniina.github.io/separo-rs/

SEPAROの実装

全体の構造

言うまでもなく、ゲームにはCUIよりもGUIの方が向いています。ゲームを作るためのGUIライブラリやフレームワークは多くありますが、もう一つ選択肢があります。ウェブページです。

この二つを比べると、Webページの方が試してもらいやすいのではないでしょうか。バイナリで配布する場合、そのバイナリはユーザーの環境で走る必要があるので、ユーザーは明示的にダウンロードし、インストールし、実行しなければなりません。対してWebページは簡単です。リンクをクリックするだけでブラウザが自動的に全てを済ませてくれるので。

また、バイナリは複数のOSで動く必要があり、クロスコンパイルして配らねばなりません。通常、複数のOSで正しく動作するGUIソフトウェアを書くのは難しいので、SEPAROを試しに遊んでみたいと思っているユーザーの一部が実行時エラーのせいでやる気をなくしてしまうかもしれません。

もちろん、Webページも環境ごとの互換性問題に無縁なわけではありません。複数のブラウザがあり、その間の互換性が問題になることはあります。とはいえ、もしページのデザインをそこまで気にしないのなら、Webページの方が簡単ではないでしょうか。

GUIをWebページとして実装する以上、UI部分はjavascriptで実装するしかありません。しかし私はjavascriptにそこまで詳しくないので、UI以外の部分、つまりゲームのルールとAIは別の言語で実装したいところです。 javascriptと他の言語を繋ぐ場合、そのコードをwebassemblyにコンパイルするのが現代的なアプローチでしょう。というわけで、ゲームとAIはRustで実装し、wasm-packを使ってビルドすることにしました。

盤の実装とスコアの計算

プレイヤーの手が適切かどうかを判定するには、各交点に石があるか、あるなら何色か、そしてどの色の根がどの向きに伸びているかを覚えておけば十分です。なので、Board構造体は以下のデータを持つことになります。

1
2
3
4
5
6
7
8
pub struct Grid {
    color: Option<Color>,
    roots: ArrayVec<[Dir; 4]>,
}
pub struct Board {
    width: usize,     // == 9, 普通は
    grids: Vec<Grid>, // 9x9 == 81要素
}

ではスコアを計算するにはどうしたらいいでしょうか？ SEPAROのスコアはプレイヤーが盤面をいくつに分割したかで決まります。分割されている領域の数を数える、という問題は、それ以上分割できない最小単位の領域をグラフのノードに、その間の繋がりをエッジに置き換えることで、グラフ中にある連結成分（極大で連結な部分グラフ）の個数を数える問題に帰着します。グラフ中の連結成分は簡単な幅優先探索で数えられるので、そのように変換すれば解けたも同然です。

プレイ中の盤面を見れば、盤のマス目は最大で4つの小さな直角二等辺三角形に分割でき、それ以上分割されることはないことがわかります。つまり、以下の図に示すようなグラフがあれば、分割された領域の数を数えることができるということです。小さな水色の円がグラフのノードを、それを繋ぐ細く黒い線がグラフのエッジを表しています。太い青線が青の根を表しており、それが通っている箇所のエッジは取り除かれています。

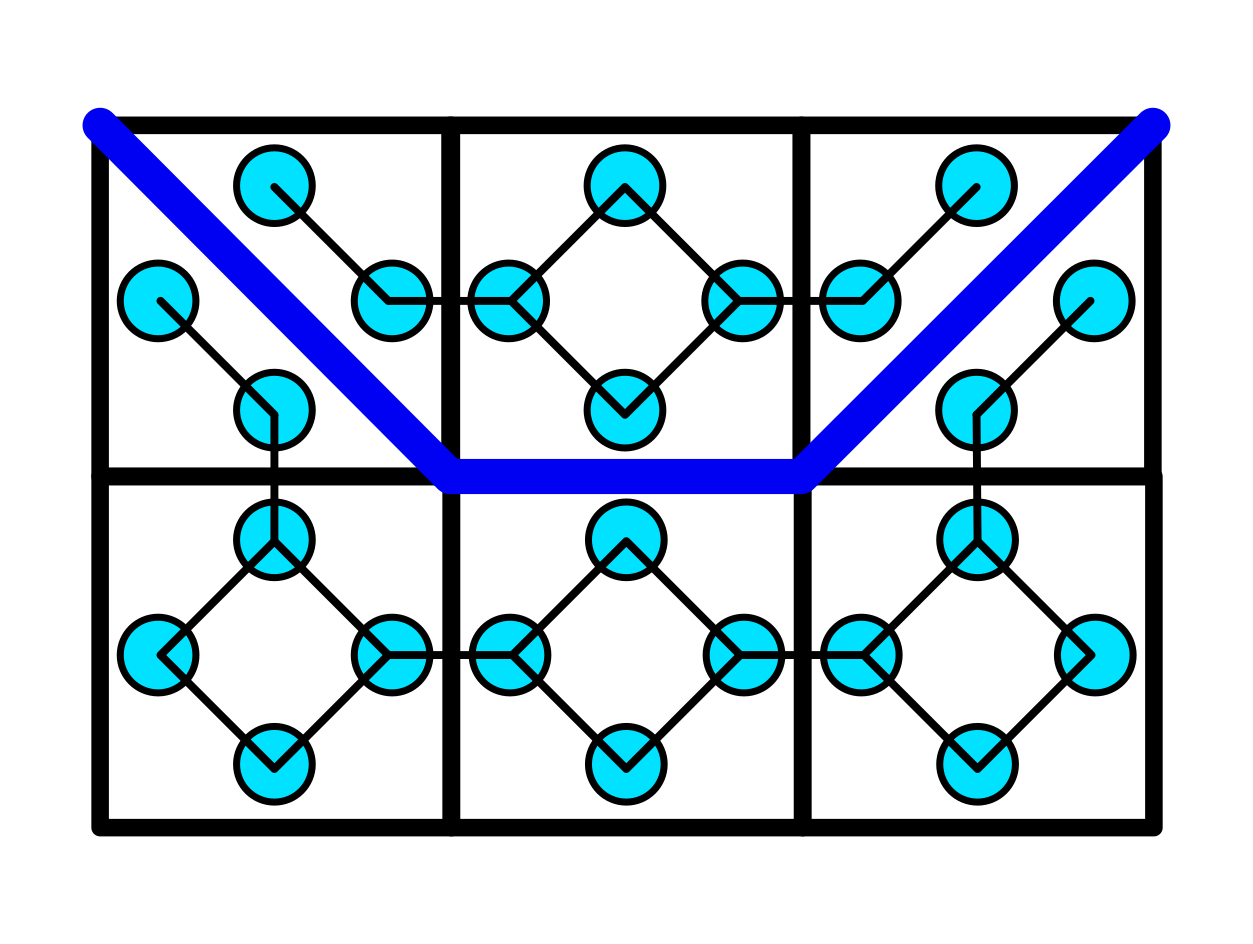
この表現にはもう一つメリットがあります。ノードが対応している微小領域の面積が全て同じなので、分割領域の面積が対応する連結成分に属するノードの数と比例することです。このため、ノードの個数を数えるだけで分割領域が小さすぎないか確認することができるわけです。

最終的に、このグラフをBoardに持たせることにしました。新たな根が伸びたときには、対応するエッジをこのグラフから取り除きます。グラフがredとblueで二つあるのは、赤と青のスコアが独立に計算されるためです。

1
2
3
4
5
6
pub struct Board {
    width: usize,     // == 9 normally
    grids: Vec<Grid>, // 9x9 grids
    red:   Graph,     // to calculate score
    blue:  Graph,     // ditto
}

Webページでの盤面の描画には<canvas>要素を使うことにしました。 Rustからjavascriptへのデータの受け渡しの方法として、rustwasmのtutorialでは、javascriptからwebassemblyのメモリ領域に直接アクセスする方法が紹介されています。もちろんそれが最も高速な方法なのでしょうが、今回はそうはせず、単純に盤面の状態をJSONにエンコードしてStringとして渡すことにしました。盤面を60FPSで描画するわけではないので、描画自体がホットスポットになることはないと判断したからです。

この実装とウェブサイトでのレンダリングを実装するのにまる一日かかりました。

AIの実装

打てる手からランダムに一つ選ぶプレイヤーを実装するだけで、対戦自体はできるようになるでしょう。しかしそれでは人間を楽しませるほどには強くなりません。

AIはプレイヤーの挙動に反応して意思決定を下さなければなりません。ここでいう意思決定は、次にどのような手を打つか、つまり次に伸ばす根はどれかを決めることです。このような場合、AIは次に打てる手のスコアを計算し、最もスコアが高いものを選びます。なので盤面の状態を取ってスコアを返すような評価関数が必要です。そのような評価関数が手に入ってしまえば、後は簡単です。次に打てる手をリストアップして、その手を打った後の盤面のスコアを計算し、最も良い手を選ぶだけです。

問題は、そのような関数をどうやって作るかです。 SEPAROは将棋と違って石に違いがありません。次に打てる手の数やその時点でのスコアは重要な要素になるでしょうが、その間のバランスを取るのは自明なことではありません。また、打つ手の価値も盤面の状態によって変わります。もしある根が盤面を分割できないなら、基本的にはその根に意味はありません。しかし、もしその根が相手が必要な根を邪魔できるのなら、価値が生まれてきます。

SEPAROは誕生から日の浅いゲームなので、どのような手が良い手なのかはまだ誰も知りません。評価関数の設計は私の手には余りました。なので、定石などの知識を必要としない評価アルゴリズムが必要になったわけです。

もちろん、ニューラルネットワークを使うこともできたでしょう。ニューラルネットワークは言ってしまえば近似関数なので、ボードの状態を取って最良の手を返すような関数を学習させることもできたはずです。とはいえ私はさほど計算資源を持っていませんでしたし、早く遊びたかったので、より古典的なアプローチを取ることにしました。

モンテカルロSEPARO

最もわかりやすいスコアは勝率です。しかし、勝率をどうやって計算したらよいのでしょう？

単純な方法として、互いに独立なシミュレーションを複数回行って、その結果で勝率を近似するというものがあります。ゲーム終了までの手をシミュレーションすれば、どちらが勝つか簡単に判定でき、ゲームのサンプルが手に入ります。そのようなサンプルを大量に集めれば、AI側が何回勝ったかで勝率を近似することができます。

ゲームをシミュレーションする最も簡単な方法は、打てる手の中から常にランダムに選ぶというものです。もちろんこれが最強のアルゴリズムというわけではありませんが、それでも初心者になら勝つこともあります。

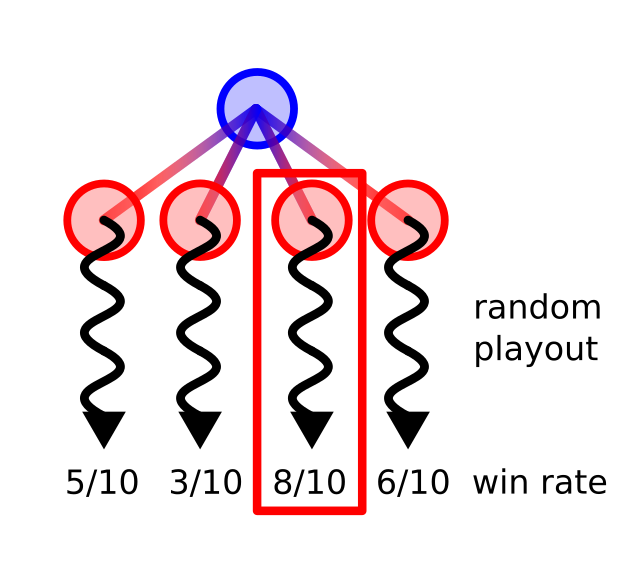
このような、乱択を繰り返して（近似的な）答えを得る手法は、カジノで有名な街の名前を取ってモンテカルロ法と呼ばれます。

モンテカルロ木探索

この近似の精度はシミュレーションの現実味に依存します。もしシミュレーションの中でプレイヤーが普通あまり選ばれないような手を選んでいた場合、その勝率も信頼できません。当然ながら、ランダムな手を選ぶシミュレーションは、人間が相手の場合あまり現実的とは言えないでしょう。

より現実的なシミュレーションを行うには、それぞれの盤においてどの手が選ばれやすいか知っておく必要があります。手が選ばれる確率を計算してくれるような関数はもちろんないので（それがそもそもの問題なわけです）、計算した勝率を使ってうまくやる必要があります。

モンテカルロ木探索は、探索木を構築して最良の手を探すアルゴリズムです。探索木のノードは親ノードで打ち得るそれぞれの手に対応しています。各ノードについて、その下のサブツリーの情報を合計すれば、そのノードの勝率が得られることになります。

モンテカルロ木探索は以下のステップから構成されています。

現在の盤面に対応する根ノードから始めて、最もスコアの高い子ノードを選びながら葉ノードまで辿っていく
もし今までその葉ノードに事前に定めた回数以上訪れていたら、その葉ノードに子ノードを付け足す。
葉ノードからランダムプレイアウトを実行し、全ての祖先ノードの勝率を更新する。

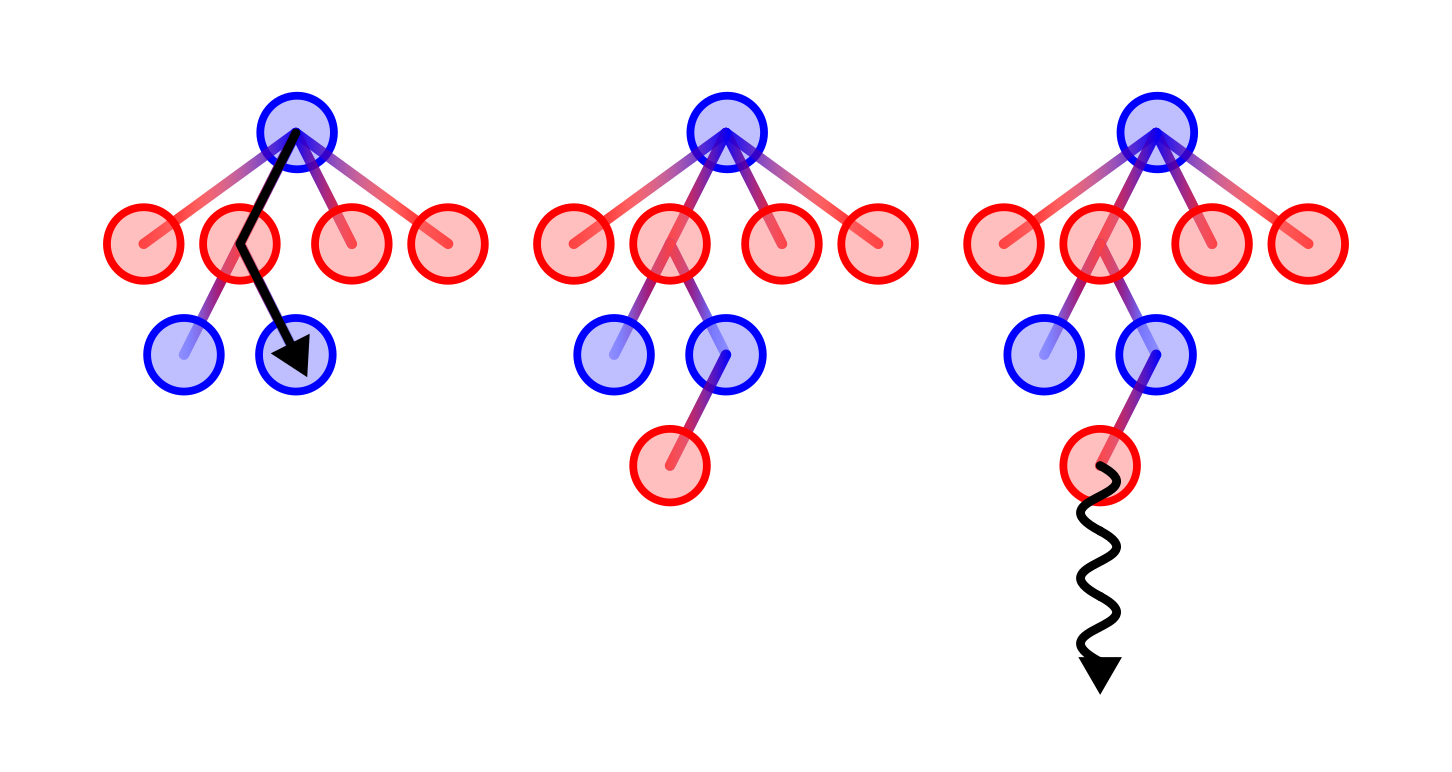
プレイヤーが双方ともに勝率を最大化しようとしていると仮定すれば、勝率が高くなるような手が選ばれる確率が高いので、勝率の高いノードをよく調べるべきでしょう。このアルゴリズムは自然にそれを達成します。このアルゴリズムは探索中は子ノードの中から最もスコアの高いノードを選んでいくので、よく訪れられるノードは高いスコアを持っていることになります。よく訪れられるノードから木が深くなっていくので、より多くのサンプルがよく訪れられるノード以下で収集されることになります。

問題は、このアルゴリズムは常にスコアが最大のノードを選ぶので、偶然勝率が高くなっただけのノードが重点的に調べられる可能性があることです。これを避けるため、Levente KocsisとCsaba Szepesváriによって2006年に提案されたUpper conficence bound 1 applied to trees (UCT)アルゴリズムを採用しました。 UCTアルゴリズムはノードを選ぶ際に、Peter Auer、Nicolò Cesa-Bianchi、Paul Fischerによって2002提案されたUCB1と呼ばれる以下のスコア関数を使用します。

\[ \mathrm{score}(\mathrm{node}) = \frac{w_i}{n_i} + c\sqrt{\cfrac{\ln N_i}{n_i}} \]

ここで、\(w_i\)はそのノード以下での勝った回数を、\(n_i\)はそのノード以下で行われたランダムプレイアウトの回数を示しています。なので第一項\(w_i/n_i\)はそのノードの勝率を表しています。 \(N_i\)は今選ぼうとしているノードの親ノードで行われたランダムプレイアウトの総数を表しており、\(c\)は経験的なパラメータです。第二項は、一種の「エラーバー」のようなもので、そのノードに割かれたサンプルが少ないほど大きな値になります。なので、第一項と第二項の和はある意味で勝率の信頼できる上限を表しているわけです。

このUCB1スコアは多腕バンディット問題のために開発されました。多腕バンディット問題は賞金の期待値が不明な多数のスロットマシンから最大の報酬を得るための戦略を考える問題です。勝率がわからない手の中から勝率が最大になるような手を選択するという問題は、多腕バンディット問題そのものです。

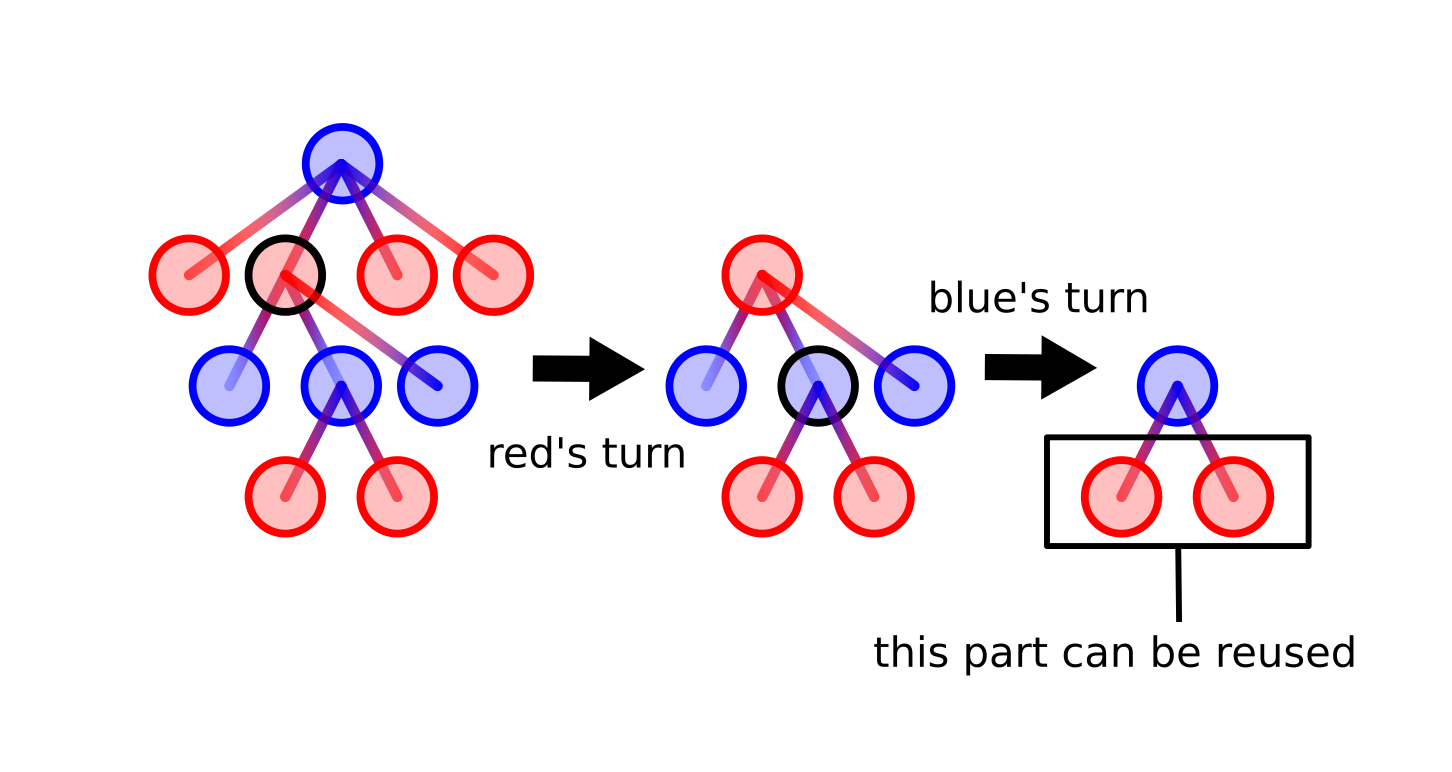
モンテカルロ木探索を実装するにあたって、アルゴリズムをより強くするために前の手で行った探索の結果を使いまわせるようにしました。しばらく探索して木を深くしたあと、アルゴリズムは根ノードの子ノードから次の手を選びます。その子ノード以下のサブツリーを次の手で再利用できることは明らかです。再利用することによって意思決定に使われるサンプルの数は毎回増えていき、より鋭い手を選べるようになります。もちろん自分の手番の最初に相手がどの手を打ったかを探索木のなかから探さなければならないわけですが。

このアルゴリズムはしばらくの間、私はおろかSEPAROの考案者であるTakeshi Suwaですら勝てない、人類よりも強いソフトウェアでした。

Conclusion

レポジトリを公開すると、ある程度の人数がSEPAROで遊んでくれたようでした。最初の日にはまだUCTを打ち破る人間は現れませんでした。しかし次の日には、私の友人の一人であるSuguru Katoが、UCTをダブルスコアで打ち破り、不思議なことにその後は多くの人がUCTに勝てるようになりました。人類の学習能力は機械にとって脅威です。

このことを通じて、プレイ可能なAIはボードゲームを誰かに教える際にも役立つことがわかりました。人間が遊びたくなったとき、AIは時間を問わず遊んでくれます。また、これは既にメジャーなボードゲームで行われていますが、AIとの、またAI同士の対戦からも定石に関する様々な考察が得られます。適度な強さのAIは、ゲームを学ぶ上でも強くなる上でも、とても役に立つ存在と言えるでしょう。

Acknowledgement

まずはSEPARO自体を使用することを快く許可してくれたT. Suwaに、そしてこのコードをSafariでも動作するよう修正してくれたS. Katoに、また英語版の草稿を読んで大量の文法ミスを発見してくれた同僚であるD. Ugarteに、感謝します。