Accuracy of Rsqrt and Weird Shadows in Ray Tracing

約一年半前、Rustを学んでいたとき、有名なレイトレーシングの教科書“Ray tracing in one weekend”を参考にレイトレーサを書いたことがあります。 この本はとても平易かつ丁寧で、本当に2日でレイトレーサを書き上げられたのですが、最適化を試みたときに少し妙なことに出くわしました。 しばらく前にもその原因を調べたことがあるのですが、今回はさらにもう一歩踏み込んでみようと思います。

Background: rsqrt instruction

3DCGの分野では、有名な最適化テクニックの一つに高速逆数平方根があります。 これはベクトルの長さを規格化するときに計算する \(1/\sqrt{x}\) を高速に近似計算するアルゴリズムです。

今日のx86_64 CPUでは、この目的のためにより精度の高いrsqrtss, rsqrtps命令が実装されています。 sqrtと割り算の組み合わせをrsqrtssに置き換えることで、ある程度の高速化が見込めるでしょう。

Rustでは、std::arch::x86_64を使うことでイントリンシックを呼ぶことができます。 個々の命令の意味を知るには、Intel Intrinsics Gudeが便利です。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

use std::arch::x86_64::_mm_set_ss;
use std::arch::x86_64::_mm_rsqrt_ss;
use std::arch::x86_64::_mm_cvtss_f32;

impl Vector3 {
    pub fn rlen(self) -> f32 {
//         original implementation
//         1.0 / self.len()
        let lsq = self.len_sq();
        unsafe {
            _mm_cvtss_f32(_mm_rsqrt_ss(_mm_set_ss(lsq)))
        }
    }
}

この変更を加えて再度実行すると、以下のような画像が出てきました。

上の画像にはなかった同心円状の影が出ていることがわかると思います。 同心円状のパターンから、カメラから飛ばすレイの長さによるエラーではないかと推測できます。 この実装ではレイを作るときは必ず規格化しているので、rsqrtss命令の誤差が蓄積した結果であることも想像がつきます。 実際、通常の割り算と平方根に置き換えるとこのアーティファクトも消えます。

Observation: pattern of errors

もしレイの長さを大きめに計算してしまっていたなら、レイと物体が衝突する位置を遠めに取ってしまい、衝突点が物体に埋もれることになります。 物体内部から投射されるレイは、物体が透明でない限り外に出ることはできません（A）。 そうなると、レイが光源にヒットしなかった場合（図B）と区別がつかないので、そのピクセルは影と判定されるでしょう。 これが暗くなっている原因ではないかと考えられます。

この「カメラから飛ばすレイの長さを計算するときのrsqrtssの誤差が原因」という仮説を検証するため、カメラから飛ばしたレイの長さを計算し、誤差をレイトレーシングの画像と同じようにしてプロットしてみましょう。 rsqrtssがレイの長さを長めに計算してしまう場合のみ、その相対誤差をログスケールでプロットすることにします。

思っていたよりも複雑な模様が出てきました。

ですが、よく考えると、レイトレーシングではノイズを減らすためにいくつかの工夫をしています。 例えば、あるピクセルの色はスクリーンのうちそのピクセルに対応する領域を通るレイの色によって決まるわけですが、これを決めるときはそのピクセルを通る何本かの異なるレイを飛ばし、平均を計算しています。 この平均によって、ノイズの局所的なパターンが消えているのではないでしょうか。

これを確かめるため、ピクセルの色を決めるときは必ずピクセルの真ん中を通るレイを考えるようにしてみました。 すると、影のパターンはほぼノイズのパターンと一致したように見えます。

また、これほど深刻ではないにせよ、浮動小数点数の計算において誤差はつきものなので、通常はレイが飛び始めた直後に起きた衝突は無視されます。 上の画像では誤差を強調するために\(10^{-5}\)としています。仮説が当たっていれば、これを小さくすればこのアーティファクトはより深刻に、大きくすれば問題はなくなっていくはずです。

許容誤差を0にしてみましょう。

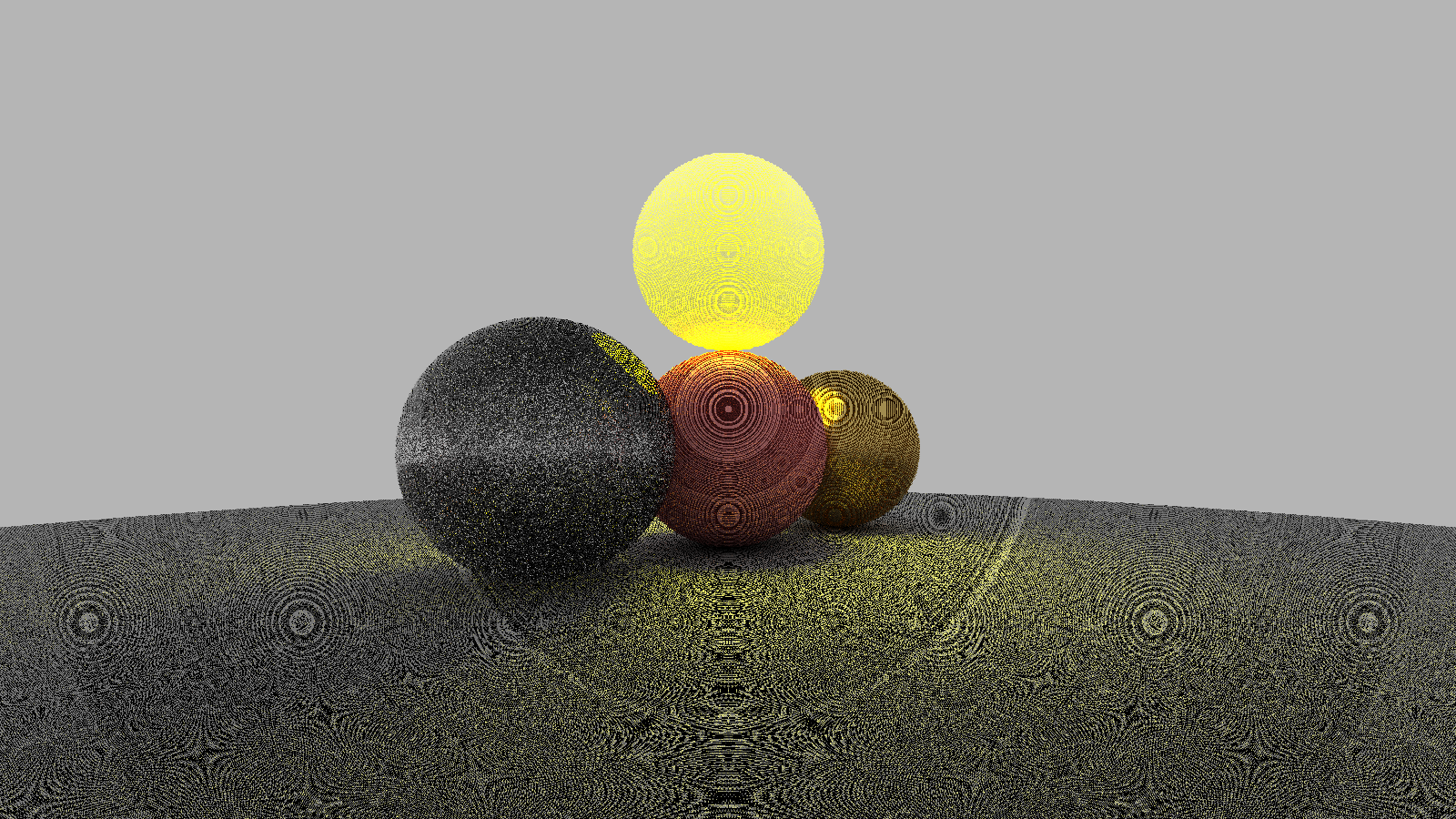
逆に、このアーティファクトが消えるくらいまで、例えば0.05にしてみましょう。

許容誤差を大きくした場合は、一見問題ないように見えますが、実際に影になるはずのところが少し明るくなってしまっています。 例えば、中央のピンク色の球体の下の影がピンク色になっています。

Conclusion

この結果を見ると、許容誤差を大きくすることでこの問題に対応しようとすると、別のところで問題が出てきてしまうようです。 となると、もっとも自明な解決策はrsqrtを使わないことでしょう。ですが、他にも方法はあります。

もともとの高速逆数平方根のアルゴリズムは、ビット演算と少しの浮動小数点数演算を組み合わせたものでした。 この浮動小数点数演算は、ニュートン法の実装になっています。ビット演算で得られた近似値から始めて、ニュートン法を一回適用することで精度を上げているわけです。 同じ方法がrsqrtの結果に対しても使えるはずです。

1
2
3
4
5
6
7
8
9

impl Vector3 {
    pub fn rlen(self) -> f32 {
        let lsq = self.len_sq();
        let r = unsafe {
            _mm_cvtss_f32(_mm_rsqrt_ss(_mm_set_ss(lsq)))
        };
        r * (1.5 - lsq * 0.5 * r * r)
    }
}

こうすると、十分な精度が担保され、アーティファクトは消えます。

手元でこの画像を生成してみたところ、sqrt版との実行時間にsignificantな差はありませんでした。 なので、可読性と速度の両方を考慮したとき、最良の選択肢は単に1/sqrt(x)を使うことなのかもしれません。 とはいえ、今回はちゃんと統計的なベンチマークを取ったわけではありません。 それに、今回と異なる場合は、例えばGPUやSIMD命令を使った場合などは、結果も変わってくるかもしれません。

この結果がレイトレーシングで奇妙な影に困っている人の助けになれば幸いです。